Welcome to the Computational Physics Group
Atomistic simulation methods are powerful tools for studying condensed matter systems. Due to the rapidly increasing speed of computers, simulation has become a very active field, offering numerous opportunities to enhance methods and explore new applications. We develop better algorithms for atomistic calculations and apply them to challenging problems. In particular, we perform structure predictions to find new materials that might be useful for novel technologies. The research has an interdisciplinary character, involving physics, mathematics, chemistry, and computer science. In this context, our work is based on a wide range of existing methods such as density functional calculations, machine learning, and Monte Carlo simulations.
New Publications and preprints
Implications of the multi-minima character of molecular crystal phases onto the free energy
In recent years, significant advancements in computational methods have dramatically enhanced the precision in determining the energetic ranking of different phases of molecular crystals. The developments mainly focused on providing accurate dispersion corrected exchange correlation functionals and methods for describing the vibrational entropy contributions to the free energy at finite temperatures. Several molecular crystals phases were recently found to have of multi-minima character. For our investigations we highlight the multi-minima character in the example of the molecular crystal consisting of N-(4-Methylbenzylidene)-4-methylalanine. We explore its potential energy landscape on the full DFT level or with a machine learned potential that was fitted to DFT data. We calculate not only many local minima but also exact barriers along transformation pathways to demonstrate the multi-minima character of our system. Furthermore, we present a framework, based on the quantum superposition method, that includes both configurational and vibrational entropy. As an example, we show for our system that the transition temperature between two of its phases is afflicted by an error of about 200 K if the multi-minima character is not taken into account. This indicates that it is absolutely essential to consider configurational entropy to obtain reliable finite temperature free energy rankings for complex molecular crystals.
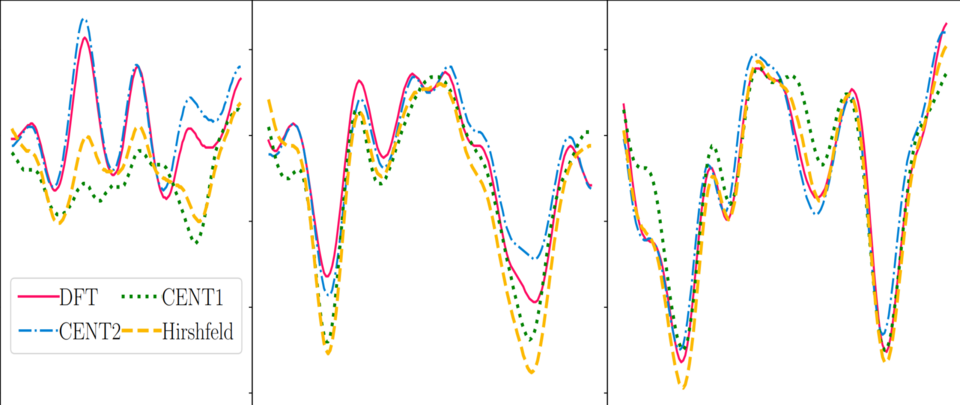
Accuracy of Charge Densities in Electronic Structure Calculations

J. Chem. Phys. 162, 094103 (2025)
Accurate charge densities are essential for reliable electronic structure calculations because they significantly impact predictions of various chemical properties and in particular, according to the Hellmann-Feynman theorem, atomic forces. This study examines the accuracy of charge densities obtained from different DFT exchange-correlation functionals in comparison with coupled cluster calculations with single and double excitations. We find that modern DFT functionals can provide highly accurate charge densities, particularly in case of meta-GGA and hybrid functionals. In connection with Gaussian basis sets, it is necessary to use the largest basis sets available to obtain densities that are nearly basis set error free. These findings highlight the importance of selecting appropriate computational methods for generating high-precision charge densities, which are for instance needed to generate reference data for training modern machine learned potentials.
Noise Tolerant Force Calculations in Density Functional Theory: A Surface Integral Approach for Wavelet-Based Methods

J. Phys. Chem. A 2025, 129, 5, 1469–1477
We introduce a method for computing quantum mechanical forces through surface integrals over the stress tensor within the framework of density functional theory. This approach avoids the inaccuracies of traditional force calculations using the Hellmann-Feynman theorem when applied to multiresolution wavelet representations of orbitals. By integrating the quantum mechanical stress tensor over surfaces that enclose individual nuclei, we achieve highly accurate forces that exhibit superior consistency with the potential energy surface. Extensive benchmarks show that surface integrals over the stress tensor offer a robust and reliable alternative to the direct use of the Hellmann-Feynman theorem for force computations in DFT with discontinuous basis sets, particularly in cases where wavelet-based methods are employed. In addition, we integrate this approach with machine learning techniques, demonstrating that the forces obtained through surface integrals are sufficiently accurate to be used as training data for machine-learned potentials. This stands in contrast to forces calculated using the Hellmann-Feynman theorem, which do not offer this level of accuracy.
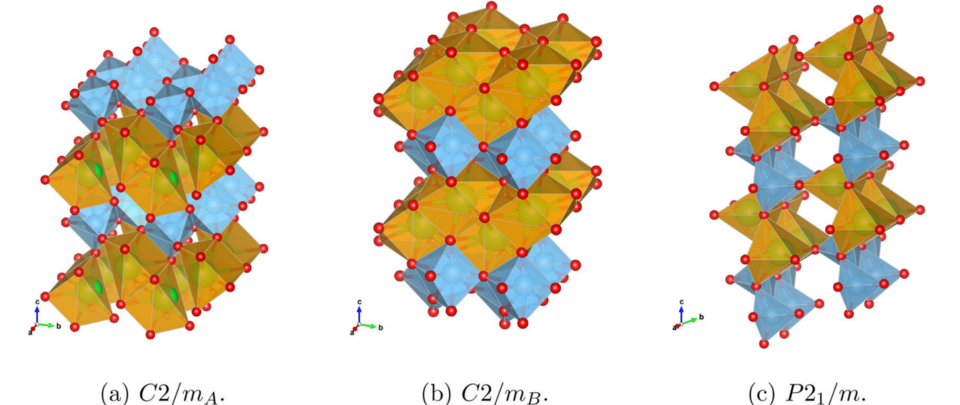
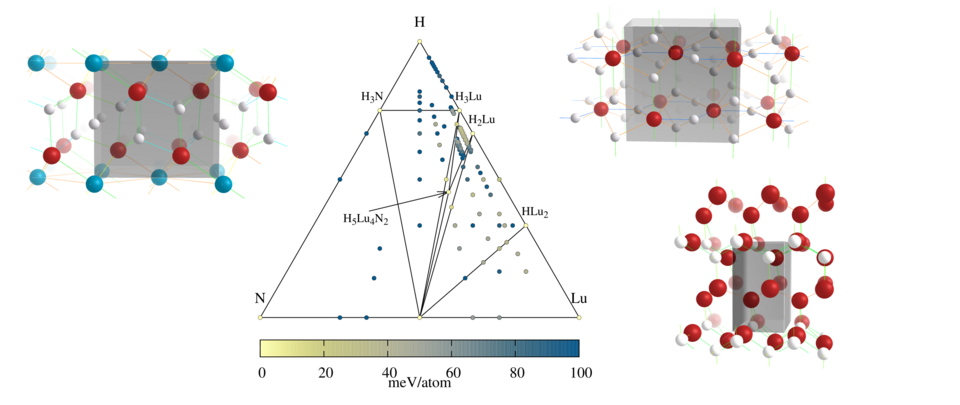
Entropic stabilization of a structurally tolerant phase: The ionic phase of lithium alanate

https://doi.org/10.21203/rs.3.rs-4318358/v1
In materials simulations, formation energies can provide valuable information about the stability of different crystal polymorphs. However, to obtain a complete picture, it is often essential to go beyond simple energetics and include free energies into the analysis as many crystal phases are stabilized by entropic contributions and phase transitions at finite temperatures are common. Traditionally, free energies of crystalline solids are computed through an analysis of the phonon band structure which is calculated within the harmonic approximation considering only the crystalline unit cell and its replication. But also methods that go beyond the harmonic approximation consider only one periodic structure to calculate free energies. We show that such an approach can overlook substantial configurational free energy contributions and does not allow us to reach a well defined thermodynamic limit. To overcome these problems, it is necessary to generate large periodic cells that can represent not only the perfect crystalline structure but also a very large number of defect structures. Only with a configurational density of states that is well converged with respect to the size of the cell, it is possible to obtain reliable estimates of phase transition temperatures. We illustrate this effect for lithium alanate where the configurational entropy contribution of the structurally tolerant ionic phase reduces the transition temperature to the polymeric phase by 150 K.
Accelerating fourth-generation machine learning potentials by quasi-linear scaling particle mesh charge equilibration

J. Chem. Theory Comput. 2024, 20, 16, 7264–7271
Machine learning potentials (MLP) have revolutionized the field of atomistic simulations by describing the atomic interactions with the accuracy of electronic structure methods at a small fraction of the costs. Most current MLPs construct the energy of a system as a sum of atomic energies, which depend on information about the atomic environments provided in form of predefined or learnable feature vectors. If, in addition, non-local phenomena like long-range charge transfer are important, fourth-generation MLPs need to be used, which include a charge equilibration (Qeq) step to take the global structure of the system into account. This Qeq can significantly increase the computational cost and thus can become the computational bottleneck for large systems. In this paper we present a highly efficient formulation of Qeq that does not require the explicit computation of the Coulomb matrix elements resulting in a quasi-linearly scaling method. Moreover, our approach also allows for the efficient calculation of energy derivatives, which explicitly consider the global structure-dependence of the atomic charges as obtained from Qeq. Due to its generality, the method is not restricted to MLPs but can also be applied within a variety of other force fields
Performing highly efficient Minima Hopping structure predictions using the Atomic Simulation Environment (ASE)

In materials science, the quest to find stable low energy structures is of great significance. Over the past two decades, the Minima Hopping algorithm has emerged as a successful tool in this pursuit. We present a robust, user friendly and efficient implementation of the Minima Hopping algorithm as a Python library. Our implementation significantly accelerates the exploration the potential energy surfaces, leveraging an MPI parallelization scheme that allows for multi level parallelization. In this scheme, multiple Minima Hopping processes are running simultaneously communicating their findings to a single database and, therefore, sharing information with each other about which parts of the potential energy surface have already been explored. Also multiple features from several existing implementations such as variable cell shape molecular dynamics and combined atomic position and cell geometry optimization for bulk systems, enhanced temperature feedback and fragmentation fixing for clusters are included in this implementation. Finally, this implementation takes advantage of the Atomic Simulation Environment (ASE) Python library allowing for high flexibility regarding the underlying energy and force evaluation.
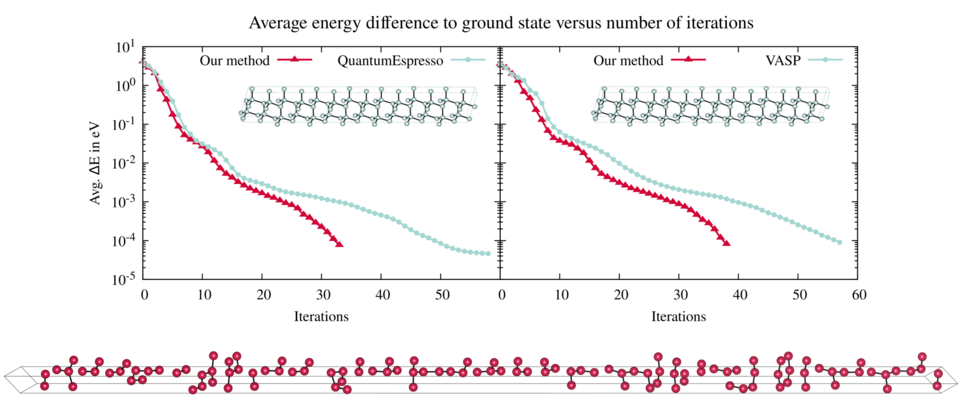
Efficient variable cell shape geometry optimization

Journal of Computational Physics: X 17 (2023) 100131
A fast and reliable geometry optimization algorithm is presented that optimizes atomic positions and lattice vectors simultaneously. Using a series of benchmarks, it is shown that the method presented in this paper outperforms in most cases the standard optimization methods implemented in popular codes such as Quantum ESPRESSO and VASP. To motivate the variable cell shape optimization method presented in here, the eigenvalues of the lattice Hessian matrix are investigated thoroughly. It is shown that they change depending on the shape of the cell and the number of particles inside the cell. For certain cell shapes the resulting condition number of the lattice matrix can grow quadratically with respect to the number of particles. By a coordinate transformation, which can be applied to all variable cell shape optimization methods, the undesirable conditioning of the lattice Hessian matrix is eliminated.
News
1. March 2025
Xingfan Zhang, who completed his PhD in the group of Prof. Richard Catlow at UCL, has started his postdoctoral research in our group.
30. January 2025
Our prepring entitled Implications of the multi-minima character of molecular crystal phases onto the free energy has been published on ArXiv.
27. January 2025
Our paper about Noise Tolerant Force Calculations in Density Functional Theory using a Surface Integral based Approach for Wavelet-Based Methods has been published in the The Journal of Physical Chemistry A
28. November 2024
Congratulations, Hannes, on successfully defending your PhD thesis titled "Efficient Methods of Exploring the Potential Energy Surface".
25. October 2024
Marco successfully defended his PhD and is now postdoc in our group.
3. October 2024
Our preprint about Noise Tolerant Force Calculations in Density Functional Theory using a Surface Integral based Approach for Wavelet-Based Methods has been published on ArXiv.
16. August 2024
Our paper Accelerating Fourth-Generation Machine Learning Potentials Using Quasi-Linear Scaling Particle Mesh Charge Equilibration has been published online.
19.May 2024
Moritz Schäfer, a PHD student in the group of Jörg Behler from Bochum started his exchange in our group. Welcome.
5. May 2024
Moritz returned from his exchange in Tromsø, Norway where he worked with Luca Frediani on calculating accurate forces in MRCHEM
24. April
Marco's preprint is about the entropic stabilization of lithium alanates is online
13 January 2024
Marcos paper is published SoftwareX, Volume 25, February 2024, 101632